Signal Flow Graph

Signal flow graph is the graphical representation of control system in which nodes representing each of system variables are connected through the direct branches. It may be regarded as the simplified version of Block Diagram. It applies only to linear system.

Basic Terminology of Signal Flow Graph

Node :-  It represent a system variable.

Branch :- Nodes are connected by line segments called branches, these branches have associated branch gain and direction, direction is represented by arrow. A signal can transmit through the branch only in the direction of arrow.

Input Node / Source node :- It is a node having outgoing branches only.

Output Node / Sink Node :- It is the node having only incoming branches.

Note :- In a signal flow graph output can be defined from any other node by extending the it with a gain of unity.

Mixed / Chain Node :- It is a node having both incoming and outgoing branches.

Path :- It is the traversal of connected branches in the direction of branch arrow such that no node is traversed more than once. A signal flow graph can have one or more than one paths.

Forward Path :- It is a path starts from input node and end at an output node.

Loop :- It is a path which originates and terminates at the same node.

Non Touching Loop :- Two or more loops are said to be non-touching if they do not have a common node.

 

Mason Gain Formula

Transfer Function =  ⁿƩ_k=1 P_k .Δ_k / Δ

Where,

n = number of forward paths

P_k = Path gain of the forward K^th path

Δ = 1 – {Sum of loop gains all individual loops} + {Sum of gain of product of two non-touching loops} – {Sum of gain products of three non-touching loop}...........

Δ_K = It is that value of “Δ” obtained by removing all the nodes touching K^th forward path.

Calculation of transfer function by using Mason Gain formula

 

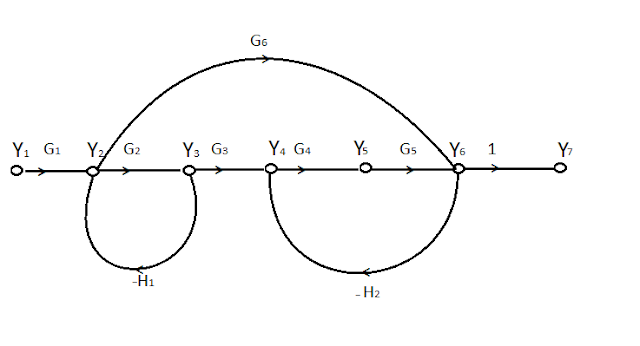
Let us take an example

In this Signal Flow Graph,

There are seven nodes these are Y₁, Y₂, Y_3, Y₄, Y_5, Y₆, Y₇. In which Y₁ is input node or source node and Y₇ is output node or sink node and rest of nodes are mixed or chain nodes.

These seven are connected through the branches having forward transfer gain G₁, G₂, G₃, G₄, G₅, 1 respectively and Y₂, Y₆ is connected through another branch have forward transfer gain G₆.

Similarly Y₂ and Y₃ is connected through a branch having negative gain H₁ and Y₄ and Y₆ is also connected through a branch having negative gain H₂.

So according to formula first we have to find the number of forward path and product of the gains of those forward paths.

There are two forward paths

P₁ = G₁G₂G₃G₄G₅1

P₂ = G₁G₆1

Then, we have to find product of gain of individual loops. So there are two individual loops these are

L₁ =  -G₂H₁

L₂ = -G₄G₅H₂

Then we have to find product of gain of two non-touching loop. There are two non-touching loop these are

L₁ =  -G₂H₁

L₂ = -G₄G₅H₂

Product of gain of these two loops is I₁ = G₂G₄G₅H₁H₂

Then we have to find Δ_k.

Δ₁ =1

Δ₂ = 1

So put all those value in Mason Gain formula after putting these values we get

^{Transfer function =}

So In this way we apply the Mason Gain formula for a particular problem.

How to convert Block Diagram into Signal Flow Graph

There are some steps which we have to follow for the conversion of Block Diagram into Signal Flow Graph

Step  :- 1   Convert all the variables, summing point, take-off point, junctions into nodes

Step :- 2 Represent all the blocks of the block diagram as branches with given directions.

Step :- 3 The transfer function of the particular block represent the gain of the corresponding branch of that particular block.

Step :- 4  Connect all the nodes with branches according to the block diagram convention and direction.

Let us take an example

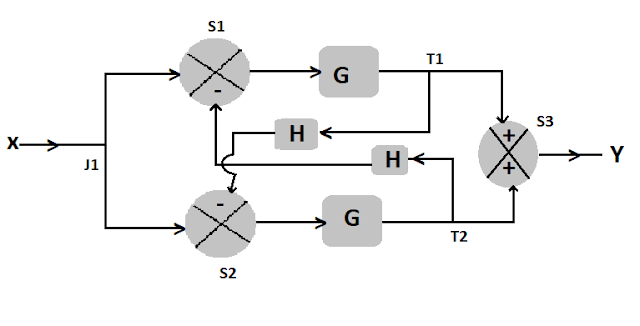Block diagram of feedback control system.

In the above diagram there are three summing points S₁ S₂ and S₃ respectively, two take-off points T₁ and T₂  and one junction point J₁.

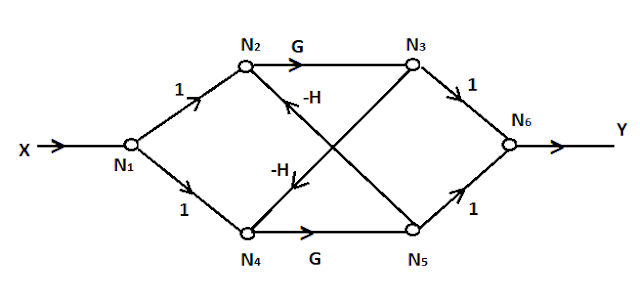
So, according to above steps convert

S₁ ――> N₂

S₂ ――> N₄

S₃ ――> N₆

T₁ ――> N₃

T₂ ――> N₅

J₁ ――> N₁

Connects all the nodes with their respective branches and assign the gain for all the branches accordingly.

# What is Control System

# Block Diagram Reduction Technique

# Construction of Root Locus