Nodal Analysis of Electric Circuits
Nodal analysis is the general technique for analyzing an electric circuit and it is based on Krichhoff’s Current law (KCL) which states that the sum of all current entering into a node is equal to the total current leaving from a node. In nodal analysis we are interested in finding node voltages. Choosing node voltage rather than voltage across elements as a circuit variable is convenient and it reduces the number of equations to be solved. In nodal analysis we have to write KCL equations for each non reference node. The number of equations derived for a circuit having n number of nodes is (n – 1).
Nodal Analysis of Electric Circuits with
Current Source
The process of a nodal analysis of an electric
circuit having current source involves the following steps to be taken
Step 1 Identify the total number of nodes in the given electric circuit. A node is point in electric circuit where two or more than two branches are connected. For example, refer the given figure.
Step 2 Out of all
the nodes, designate a node as a reference node. A reference node a common node
for all the other node against which node voltages of all the nodes measured. Generally,
the ground is taken as reference node.
Step 3 Assign
unknown voltage variables to all non-reference nodes.
Step 4 Develop
KCL equations for each non reference node (i.e. the sum of current coming
towards the node is equal to the sum of current going outwards from the node).
Step 5 Express
the driven equation in terms of nodal voltages by the help of Ohm's Law i.e.
(I = V/R) and also express any other unknown voltage and current
other than the node voltage in terms of nodal voltage.
Step 6 Arrange
the driven equation and solve them for finding the node voltage.
Let us understand these steps with the help of an
example
Consider the circuit shown in the
given figure.
According to the first step, identify
the number of nodes in the given circuit i.e. three (node 1, node 2 and
node 3).
According to second step, designate a
reference node. In the given circuit we have clearly seen that node 3 is common
for all other node (node 1 and node2) and its potential is at ground potential
that's why it is taken as reference node.
Once the reference node is selected then as per step 3 assign the voltage designation to all other non-reference nodes. In the given example we have assign V1 variable of node 1 and V2 for node 2.
After assigning variables for each node now moving forward to the next step that is develop the KCL equations for each non reference node.
I1 = i1 + i3 ………………… (1)
At node 2
applying KCL
i1 = i2 + I2
……………………(2)
According to step 5 there is no any
unknown voltage or current present in the given circuit rather than node
voltage. Actually, this happens in the circuit having dependent sources.
Write the derived equation in the
form of voltage by the help of Ohm's Law (I
= V/R).
Put these Values in equation (1) and (2)
After writing these equations in the
form of node voltages we have got two equations to be solved for the given
circuit having three nodes. As in the introduction part we discuss that in
Nodal analysis (n – 1) equations to be solved for the circuit analysis.
Nodal Analysis of Electric Circuit with
Voltage Source
Nodal analysis of an electric circuit having
voltage source connected between two non-reference nodes introduces the concept
of super-node. In an electric circuit a voltage source is connected in two
ways either it is connected between a non-reference node and a reference node
or it is connected between two non-reference nodes.
If voltage source is connected between a
non-reference node and a reference node than the node voltage of non-reference
node is equal to the voltage of the voltage source.
If voltage is connected between two
non-reference nodes than it is difficult to find the current in that branch. Hence,
KCL equation cannot be developed for such nodes. That’s why the branch having
voltage source connected between two non-reference node is considered as super-node.
Let us understand the concept of super-node the help of an example.
Consider the circuit as shown in given figure
In the given figure we saw that there are two voltage sources present in the circuit. In which one voltage source is connected between a reference (node 4) and a non-reference (node 1) and other voltage source is connected between two non-reference node (node 2 and node 3).
So, if we calculate the voltage at
node 1 it is simply equals to the voltage of the voltage source V1.
But if we drive the KCL equations for
node 2 and node 3 for calculating the node voltages we will run into some
difficulty because we do not know the current in the branch having voltage
source or there is no way by which we can express the current in the form
of voltage. So, for the convenience node 2, node 3 and voltage of source
together treated as super-node, the super-node is indicated by the region
enclosed by the broken line shown in figure. By considering it as super-node we
can apply KCL to the both node at same time.
Let us develop the nodal equations for this
circuit.
In the given circuit there are four nodes (node 1,2,3 and 4) in
which node 4 is the reference node and node 1, 2, 3 are the non-reference
nodes. As per step second assigning voltage variables for each non reference
node Va, Vb and Vc are the voltage variables
for node 1, 2, 3 respectively. Now develop the KCL equations for each
no-reference node keeping the super-node concept in mind that we have discussed
previously.
At node 1
va
= V1 discussed earlier
I
= i1 + i2 ……………….(1)
Put these values in equation 1
At node 2 and 3
Remember that node 2 and node 3 combined treated as super-node.
i1
- i3 - i4 + I1 =
0
I1 = i3 + i4 - i1
related post
#_Resistor
#_Inductor






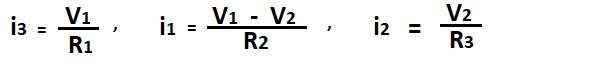













No comments:
Post a Comment
Please feel free to provide feedback and suggestions, and also don't hesitate to ask your questions.